 08-07-2009, 02:02 PM
08-07-2009, 02:02 PM
|
#1
|
|
|
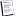 التكامل والتفاضل (مقدمة تمهيدية)
التكامل والتفاضل (مقدمة تمهيدية)
التفاضل و التكامل (باللاتينية: Calculus) فرع من فروع الرياضيات يدرس النهايات و الاشتقاق و التكامل و المتسلسلات الانهائية. وهو علم يستخدم لدراسة التغير في الدوال و تحليلها.
ويدخل علم التفاضل و التكامل في العديد من التطبيقات في الهندسة و العلوم المختلفة حيث كثيرا ما يحتاج لدراسة سلوك الدالة و التغير فيها و حل المشاكل التي يعجز علم الجبر عن حلها بسهولة.وعادة مايدرس علم التفاضل والتكامل بعد دراسة أساسيات الجبر و الهندسة و حساب المثلثات. ومن الموضوعات الرئيسية في هذا العلم هي النهايات و الكميات الموحلة في الصغر.
و ينقسم إلى هذا العلم إلى فرعين هما التفاضل و التكامل ويربط بينهما ما يعرف بالنظرية الأساسية للتفاضل و التكامل. وفى بعض الأحيان قد يستخدم الاسم تفاضل و تكامل في الاشارة إلى أي نظام يستخدم في الحسبان و يستخدم فية الرموز في التعامل مع المصطلحات و المتغيرات المختلفة مثل تفاضل و تكامل لامبدا و التفاضل و التكامل الاقتراحى و التفاضل و التكامل العلائقى و التفاضل و التكامل المؤكد.
النهايات
تهتم بدراسة اتصال الدالة و قيمتها عندما يقترب تابعها من من قيمة معينة.
بفرض أن الدالة  هي دالة حقيقية و أن هي دالة حقيقية و أن  عدد حقيقي أيضا:
عندئذ يمكن القول: عدد حقيقي أيضا:
عندئذ يمكن القول:
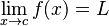 أي أن الدالة أي أن الدالة  تكون قريبة جدا حسبما نريد من تكون قريبة جدا حسبما نريد من 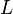 عندما تقترب عندما تقترب  من العدد c ونعبر عن ذلك لغة (أن نهاية من العدد c ونعبر عن ذلك لغة (أن نهاية  , عندما , عندما  تؤول إلى تؤول إلى  , هي , هي 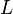 ).
التفاضل والاشتقاق
يتم اشتقاق التفاضل للدالة ).
التفاضل والاشتقاق
يتم اشتقاق التفاضل للدالة  من التعريف الرئيسي للنهاية بالعلاقة: من التعريف الرئيسي للنهاية بالعلاقة:
 التكامل
في علم الرياضيات ينقسم التكامل إلى جزئين: التكامل المحدود و التكامل الغير محدود. يتعلق التكامل المحدود بحساب الاطوال, المساحات, المنحنيات, مراكز الثقل و ما إلى ذلك من الدوال التي لها تطبيقات في شتى العلوم. من جهة أخرى يركز التكامل الغير محدود على ايجاد المعكوس الرياضي للتفاضل و لهذا السبب يسمى أيضا بالاشتقاق العكسي.
الاشتقاق العكسي
يعطى التكامل الغير محدود لتابع التكامل
في علم الرياضيات ينقسم التكامل إلى جزئين: التكامل المحدود و التكامل الغير محدود. يتعلق التكامل المحدود بحساب الاطوال, المساحات, المنحنيات, مراكز الثقل و ما إلى ذلك من الدوال التي لها تطبيقات في شتى العلوم. من جهة أخرى يركز التكامل الغير محدود على ايجاد المعكوس الرياضي للتفاضل و لهذا السبب يسمى أيضا بالاشتقاق العكسي.
الاشتقاق العكسي
يعطى التكامل الغير محدود لتابع  رياضي بالعلاقة: رياضي بالعلاقة:
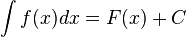 حيث حيث  التكامل المحدود
يعبر عنه بالشكل الرياضي: التكامل المحدود
يعبر عنه بالشكل الرياضي:
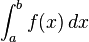 تطبيقات
لعلم التفاضل والتكامل تطبيقات لا حصر لها في علوم الفيزياء الكلاسيكية والحديثة, الكيمياء, الهندسة, الاقتصاد, الحاسوب و حتى في الطب وبعض العلوم السياسيةوالادبية. هنا بعض الامثلة:
تطبيقات
لعلم التفاضل والتكامل تطبيقات لا حصر لها في علوم الفيزياء الكلاسيكية والحديثة, الكيمياء, الهندسة, الاقتصاد, الحاسوب و حتى في الطب وبعض العلوم السياسيةوالادبية. هنا بعض الامثلة:- حساب اطوال المنحنيات, المساحات, والحجوم.
- حساب مركز الثقل, عزم القصور الذاتي, كمية التحرك, العجلة, السرعة, الإزاحة, الشغل, الطاقة.
- حساب التوزيعات و الاحتمالات المنتظمة كإحتمالية فيرمي في أشباه الموصلات, انتشار جراثيم في وسط معين تحت ظروف بيئية معينة.
- حل المعادلات التفاضلية وتطبيقاتها في الانظمة الخطية مثل البندول, دوائر الرنين الكهربائية, و أنظمة التحكم الكهروميكانيكية.
- اشتقاق الكثير من المعادلات الفيزيائية الحديثة و التي يكون من الصعب اجرائها تجريبيا.
- حساب الثوابت الرياضية إلى درجات عالية من الدقة مثل قيمة ثابت الدائرة
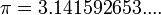 , الثابت الطبيعي , الثابت الطبيعي  وكذلك الدوال الرياضية المعقدة وامكانية برمجة هذه العمليات بواسطة الحاسوب. وكذلك الدوال الرياضية المعقدة وامكانية برمجة هذه العمليات بواسطة الحاسوب.
[عدل] تاريخ
يعتقد البعض ان علم التفاضل قد سبق التكامل كون التكامل عملية عكسية للتفاضل و هذا غير صحيح. فقد أظهرت الأدلة التاريخية استخدام التكامل بطرق غير مباشرة في حساب المساحات و الحجوم كما كان في عهد المصريين القدماء في طريقة حساب حجم الهرم الناقص. كما تبعهم اليونانيون في استخدام طريقة الاستنزاف لحساب المساحات والحجوم ثم ازدهرت هذه الطريقة في عهد أرشيميدس الذي أدخل فكرة الخبرة المكتسبة والتي تمثل جزءَ أساسيا في علم التكامل. ثم انتقلت طريقة الاستنزاف إلى الصين حيث عملوا جاهدين على ايجاد مساحة الدائرة و حجم الكرة.
وفي العصر الإسلامي استطاع ابن الهيثم استخدام طريقة تكاملية لاستنباط الصيغة العامة لمجموع متوالية حسابية من الدرجة الرابعة. ثم ابتدع الصينيون معادلات تتعامل مع التكامل, وفي الهند بدأ الاشتقاق بالظهور على يد هندي رياضي وصف التغيرات المتناهية في الصغر كما توصل اخرون لمتسلسلات شيهة بمتسلسلة تايلور.
مع ظهور عصر النهضة بدأ الغرب بتعلم وترجمة الكتب القديمة كاليونانية, الحديثة كالعربية وتطوير علوم الرياضيات, الفيزياء, الكيمياء, وبعض العلوم الأخرى وتطور علم التفاضل والتكامل بشكل خاص على يد مؤسسه إسحاق نيوتن.
منقووووووووول للفائدة
|

|

|