 09-25-2009, 01:49 AM
09-25-2009, 01:49 AM
|
#3
|
|
|
 رد: اسرار العدد باي.. (π )
رد: اسرار العدد باي.. (π )
شكراً لك على هذا الموضوع واسمح لي أن اضيف المعلومات التالية عنه:
ط أو پاي (π) أو النسبة الثابتة أو النسبة التقريبية هي ثابت رياضي يستخدم في الرياضيات والفيزياء، الرمز π مأخوذ من الحرف الإغريقي الصغير پي.
يعرف ط على أنه النسبة بين محيط الدائرة وقطرها. وهو عدد حقيقي غير كسري أي لا يمكن كتابته على شكل a / b حيث a,b أعداد صحيحة. وهو أيضاَ عدد متسامي أي غير جبري.
يعرف هذا العدد أيضا باسم ثابت أرخميدس.
 عندما يكون قطر دائرة =1، يكون محيطها= π.
ومن المعروف أن الأعداد غير النسبية لا يمكن تمثيلها بكسر عشري منته، لكن من المعتاد تقريب ط بالقيمة 3.14 أو 22 / 7.
تاريخ ط وحسابها التقريبي
حساب ط في العصور القديمة
من غير المعروف كيف ومتى اكتشف الإنسان أن النسبة بين محيط الدائرة وقطرها هي نسبة ثابتة، لكن من الأكيد أن هذه الحقيقة قد عرفت منذ قديم الزمان. فالحضارات القديمة كالحضارة المصرية والبابلية تعاملت مع ط ، كان البابليون يستخدمون التقريب 25 / 8 بينما استخدم المصريون التقريب 256 / 81.[1] ويرجع حصر قيمة π بين 22 / 7 و 221 / 73 إلى العالم اليوناني أرخميدس الذي ابتكر طريقة الاستنفاذ لحساب قيمة تقريبية للعدد ط.
في القرون التالية اهتم الفلكيون بتدقيق الحساب التقريبي ل ط، وأوجد الفلكيون الهنود والصينيون عدة صيغ للقيمة التقريبية، وشارك العلماء العرب في تحسين تلك الصيغ، فتوصل جمشيد غياث الدين الكاشي في القرن الخامس عشر لحساب قيمة تقريبية صحيحة حتى ستة عشر رقم عشري.
الجدير بالذكر أن حساب العدد ط أو π كان قد وصل به غياث الدين الكاشي ا إلى 16 مرتبة عشرية قبل ظهور الالات الحاسبة بأربعمائة سنة.
حساب ط في العصر الحديث
مع ظهور الآلات الحاسبة ثم الحاسبات الالكترونية والنظرية الرياضية للنهايات والمتسلسلات اللانهائية تحسنت قدرة العلماء على حساب قيم تقريبية للعدد ط، ووصل السجل العالمي حتى عام 2002 إلى أكثر من تريليون رقم عشري.
قيمة π التقريبية حتى 50 مرتبة عشرية:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510
صيغ حسابية للعدد ط
إحدى المعادلات المعروفة لإيجاد ط هي :
عندما يكون قطر دائرة =1، يكون محيطها= π.
ومن المعروف أن الأعداد غير النسبية لا يمكن تمثيلها بكسر عشري منته، لكن من المعتاد تقريب ط بالقيمة 3.14 أو 22 / 7.
تاريخ ط وحسابها التقريبي
حساب ط في العصور القديمة
من غير المعروف كيف ومتى اكتشف الإنسان أن النسبة بين محيط الدائرة وقطرها هي نسبة ثابتة، لكن من الأكيد أن هذه الحقيقة قد عرفت منذ قديم الزمان. فالحضارات القديمة كالحضارة المصرية والبابلية تعاملت مع ط ، كان البابليون يستخدمون التقريب 25 / 8 بينما استخدم المصريون التقريب 256 / 81.[1] ويرجع حصر قيمة π بين 22 / 7 و 221 / 73 إلى العالم اليوناني أرخميدس الذي ابتكر طريقة الاستنفاذ لحساب قيمة تقريبية للعدد ط.
في القرون التالية اهتم الفلكيون بتدقيق الحساب التقريبي ل ط، وأوجد الفلكيون الهنود والصينيون عدة صيغ للقيمة التقريبية، وشارك العلماء العرب في تحسين تلك الصيغ، فتوصل جمشيد غياث الدين الكاشي في القرن الخامس عشر لحساب قيمة تقريبية صحيحة حتى ستة عشر رقم عشري.
الجدير بالذكر أن حساب العدد ط أو π كان قد وصل به غياث الدين الكاشي ا إلى 16 مرتبة عشرية قبل ظهور الالات الحاسبة بأربعمائة سنة.
حساب ط في العصر الحديث
مع ظهور الآلات الحاسبة ثم الحاسبات الالكترونية والنظرية الرياضية للنهايات والمتسلسلات اللانهائية تحسنت قدرة العلماء على حساب قيم تقريبية للعدد ط، ووصل السجل العالمي حتى عام 2002 إلى أكثر من تريليون رقم عشري.
قيمة π التقريبية حتى 50 مرتبة عشرية:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510
صيغ حسابية للعدد ط
إحدى المعادلات المعروفة لإيجاد ط هي :
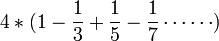 ويمكن استنتاج هذه الصيغة من متسلسلة ماكلورين للدالة قوس ظا ((بالإنجليزية: arctan)) حيث
ويمكن استنتاج هذه الصيغة من متسلسلة ماكلورين للدالة قوس ظا ((بالإنجليزية: arctan)) حيث
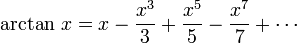 في الحقيقة لاتستخدم الالات الحسابية السلسلة السابقة (عند تعويض x =1) بسبب تقاربها البطيء ويمكن ملاحظة ذلك عند الوصول إلى رقم المليون وواحد مثلا ستكون الدقة لاتتجاوز خمس مراتب عشرية, وهكذا.
يمكن استعمال الصيغة الرياضية عند تعويضات x أكبر من الواحد للحصول على تقارب أسرع مثل:
في الحقيقة لاتستخدم الالات الحسابية السلسلة السابقة (عند تعويض x =1) بسبب تقاربها البطيء ويمكن ملاحظة ذلك عند الوصول إلى رقم المليون وواحد مثلا ستكون الدقة لاتتجاوز خمس مراتب عشرية, وهكذا.
يمكن استعمال الصيغة الرياضية عند تعويضات x أكبر من الواحد للحصول على تقارب أسرع مثل:
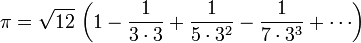 وقد استطاع جون ماشن تسريع التقارب السابق وحساب ط حتى 100 مرتبة عشرية باستخدام قانون قوس الظل: وقد استطاع جون ماشن تسريع التقارب السابق وحساب ط حتى 100 مرتبة عشرية باستخدام قانون قوس الظل:
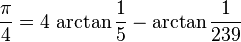 وهي الطريقة التي استعملت فيما بعد في أجهزة الحاسوب وحتى عهد قريب. هناك حسابات أخرى مثل: وهي الطريقة التي استعملت فيما بعد في أجهزة الحاسوب وحتى عهد قريب. هناك حسابات أخرى مثل: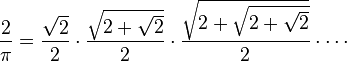  اما في العصر الحديث فقد ظهرت خوارزميات أكثر تقاربا بكثير مثل: اما في العصر الحديث فقد ظهرت خوارزميات أكثر تقاربا بكثير مثل: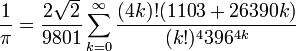 - سلسلة الاخوان تشوندوفيسكي التي سمحت لاول مرة تقريب ط لمليار مرتبة عشرية عام 1989 باستخدام الحاسوب العملاق:
 و كان لخواريزمية برنت سالامن الاكتشاف الاروع والتي تبدأ بوضع: و كان لخواريزمية برنت سالامن الاكتشاف الاروع والتي تبدأ بوضع:
 ثم المعاودة: ثم المعاودة:
 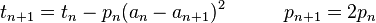 حتى تصبح an و bn متقاربة بما يكفي. ويعطى تقريب π حتى تصبح an و bn متقاربة بما يكفي. ويعطى تقريب π
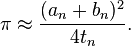 ثم اكتشف علاقة أكثر ادهاشا: ثم اكتشف علاقة أكثر ادهاشا:
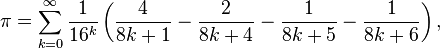 كونها بصيغة كسرية يمكن بها استخلاص الارقام السداسية عشر و الثنائية دون حساب سابقاتها وبها امكن الوصول إلى 1,000,000,000,000,000 مرتبة عشرية.
في عام 2006 استطاع سيمون بلوف توليد سلسلة من الصيغ المدهشة بوضع q = eπ]], وبالتالي كونها بصيغة كسرية يمكن بها استخلاص الارقام السداسية عشر و الثنائية دون حساب سابقاتها وبها امكن الوصول إلى 1,000,000,000,000,000 مرتبة عشرية.
في عام 2006 استطاع سيمون بلوف توليد سلسلة من الصيغ المدهشة بوضع q = eπ]], وبالتالي
 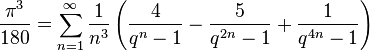 وأخرى بالشكل, وأخرى بالشكل,
 حيث q = eπ, k هو عدد فردي, و a, b, c are اعداد نسبية. اذا كانت k على الشكل 4m + 3, تصبح الصيغة بالشكل المبسط, حيث q = eπ, k هو عدد فردي, و a, b, c are اعداد نسبية. اذا كانت k على الشكل 4m + 3, تصبح الصيغة بالشكل المبسط,
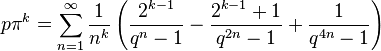 كما يمكن تمثيل ط في صيغة كسر مستمر بالشكل: كما يمكن تمثيل ط في صيغة كسر مستمر بالشكل:
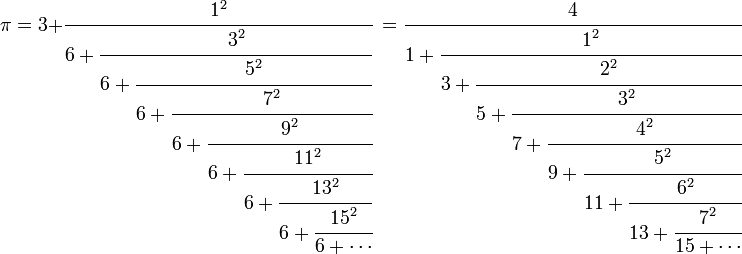 والذي يريد ان يرى الرقم باي مقرباً الى (4194304 ) خانة فليدخل على الرابط التالي وينتظر حتى يكتمل الرقم:
والذي يريد ان يرى الرقم باي مقرباً الى (4194304 ) خانة فليدخل على الرابط التالي وينتظر حتى يكتمل الرقم:
| التوقيع |
|
إِذا رُمتَ أَن تَحيا سَليماً مِنَ الأذى = وَحظك مَوفورٌ وَعِرضُكَ صَيِّنُ فَلا يَنطِقَن مِنكَ اللِسانُ بِسَوأَةٍ = فَكُلُّكَ سَوءاتٌ وَلِلناسِ أَلسُنُ وَعَينكَ إِن أَبدَت إِلَيكَ مَعائِباً = فَصنها وَقُل يا عَينُ لِلناسِ أَعيُنُ وَعاشِر بِمَعروفٍ وَسامِح مَنِ اِعتَدى = وَفارق وَلَكِن بِالَّتي هِيَ أَحسَنُ |
|

|

|